Определение расчетных усилий арочных и комбинированных систем

1. Трех- и двухшарнирные арки

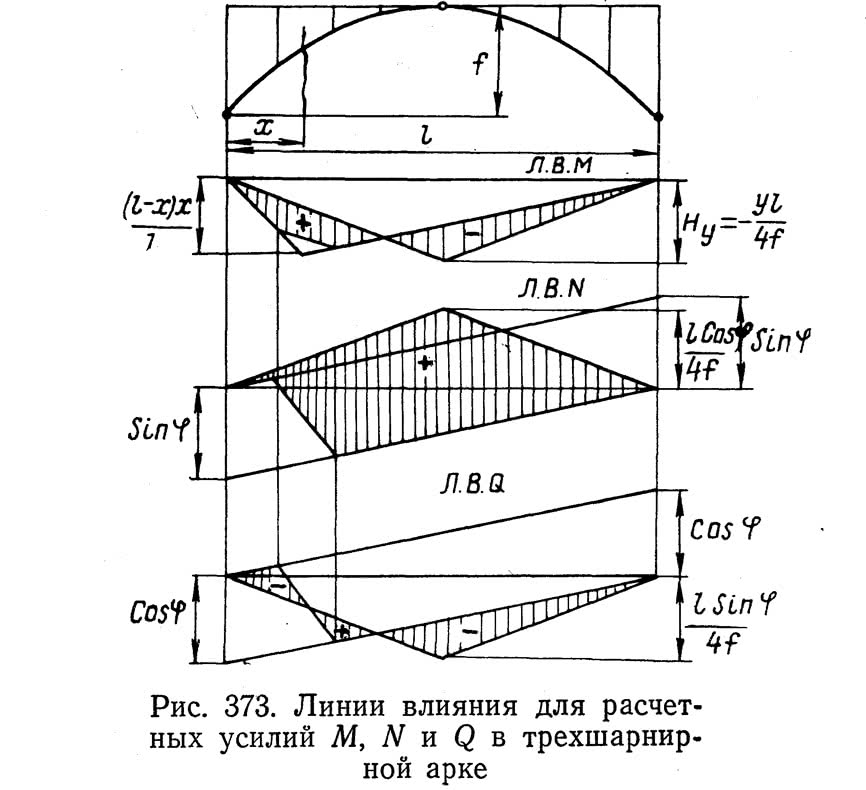
Расчетные усилия М, N и Q в сечениях сплошных трех- и двухшарнирных арок определяются равенствами:

вытекающими из условий равновесия части арок левее сечения, в котором действуют определяемые усилия (рис. 371).

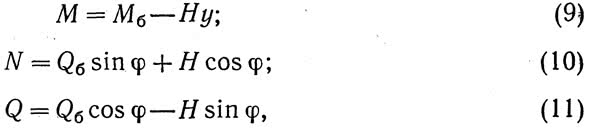
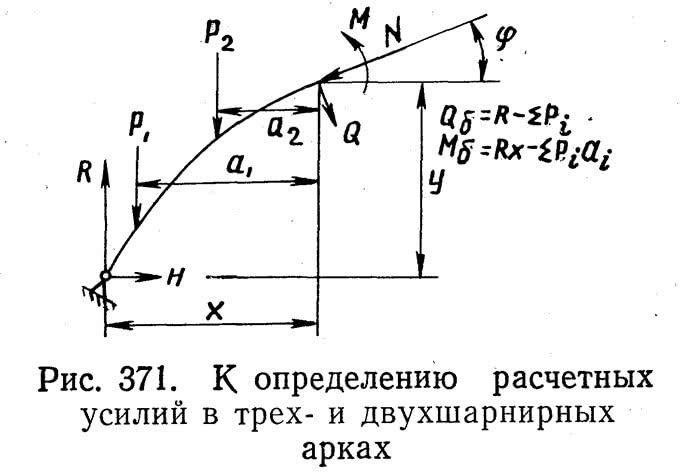
В равенствах (9)—(11) М_б и Q_б — изгибающий момент и перерезывающая сила в соответствующем сечении шарнирно опертой балки такого же пролета, как арка и также загруженной.

Ординаты линии влияния для каждого из расчетных усилий вычисляют путем алгебраического суммирования соответствующих ординат линий влияния для распора H, момента М_б и перерезывающей силы Q_б, умноженных предварительно на у, sin ? и cos ? согласно равенствам (9)—(11).

Линия влияния для распора в симметричной трехшарнирной, статически определимой арке и способ ее построения из условий равновесия показаны на рис. 372.

Линия влияния для расчетных усилий в сечении х трехшарнирной арки показаны на рис. 373.

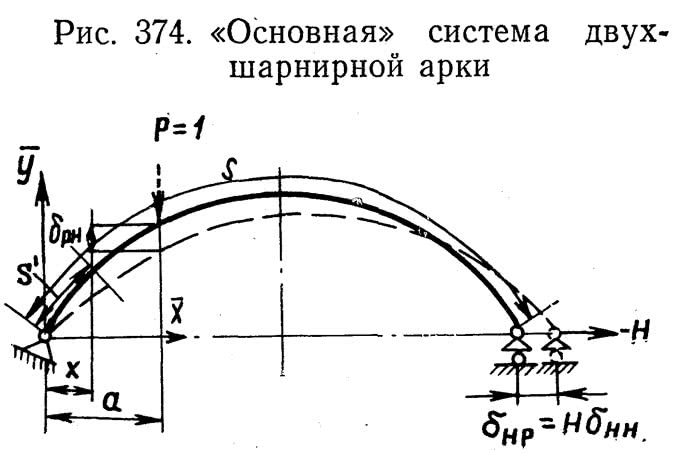
Двухшарнирная арка один раз статически неопределима. В качестве лишней неизвестной обычно выбирают распор Я. Тогда основная система (по методу сил) представит собой криволинейную балку (рис. 374), одна из опор которой имеет продольную подвижность.

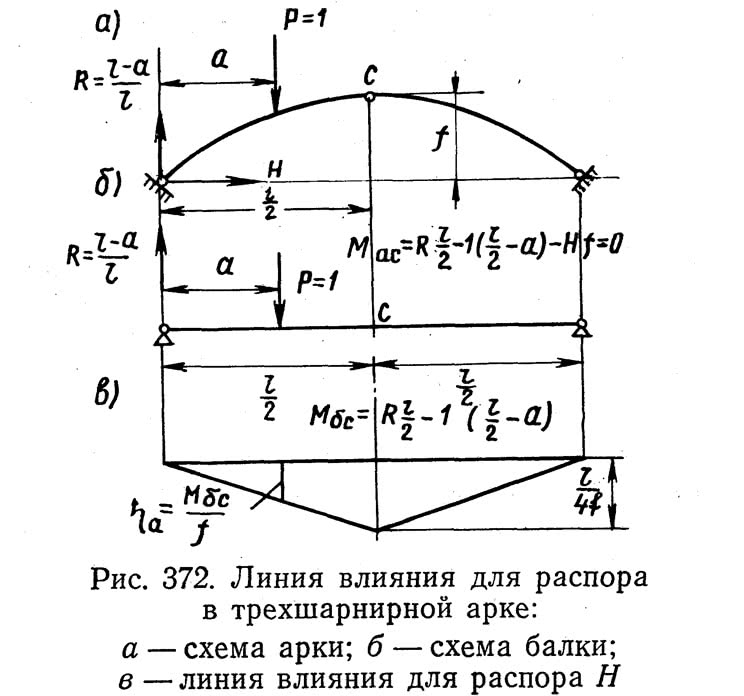
Ордината г)а линии влияния распора Я на расстоянии а от начала координат определится по формуле:

Этой формулой не учитываются слагаемые перемещений ?_рн, ?_нн, определяемые действием поперечных сил и учетом кривизны арки. В числителе отброшено также слагаемое, отражающее влияние продольных усилий на величину перемещений. Погрешности, связанные с этими упрощениями, невелики.

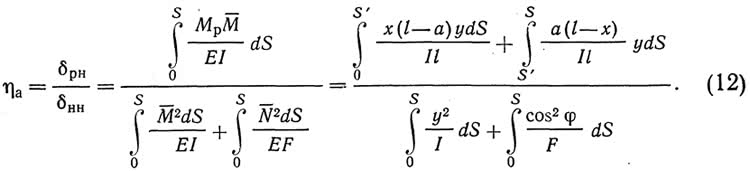
Вычисление интегралов, через которые выражены перемещения ?_рн и ?_нн, требует исходных данных о форме оси арки и о законах изменения момента инерции и площади поперечного сечения арки по длине пролета.

В дальнейшем задаемся рядом предпосылок.

Для двухшарнирной и бесшарнирной арок, а также для комбинированных схем очертание арок принято по квадратной параболе, уравнение которой принимает тот или иной вид в зависимости от взаиморасположения арки и системы координат, которое указано на всех схемах.

Для симметричной двухшарнирной арки начало координат помещено в левой пяте, и ось х направлена горизонтально вправо по линии, соединяющей пяты, а ось у вертикально вверх. В этом случае уравнение оси арки принимает вид:

Площадь поперечного сечения арок F принята во всех случаях изменяющейся по закону косинуса:

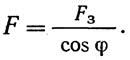
Изменяющимся по такому же закону принят и момент инерции жестких арок, работающих на сжатие с изгибом:

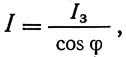
где F₃ и I₃ — площадь и момент инерции сечения арки в замке.

Момент инерции I_б балок жесткости принят по длине пролета постоянным.

Перечисленные предпосылки очень удобны для вычисления интегралов и обычно близко соответствуют действительности, кроме закона косинуса для изменения момента инерции в арках с шарнирами в пятах, в которых моменты на участках от четвертей пролета к пятам не возрастают, а уменьшаются. Однако по исследованиям проф. И. П. Прокофьева¹ такое несоответствие изменения изгибающих моментов изменению моментов инерции сопряжено с несущественной погрешностью в определении распора.

Приводимые в настоящей главе расчетные формулы достаточно точны для эскизного проектирования. При необходимости уточнения расчетов можно использовать метод «упругих грузов», применяемый при любом очертании арок и любом законе изменения сечений их по длине пролета. Этот метод излагается в курсах строительной механики.

Интегрирование выражения (12) приводит к простому результату:

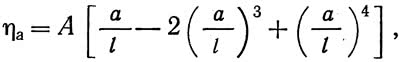
где для арок с пологостью f/l>1/5

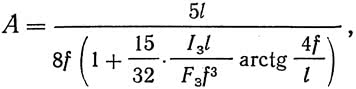
а для пологих арок f/l2?=1,

Из последних формул видно, что А — коэффициент, постоянный для всех ординат.

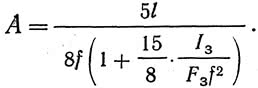
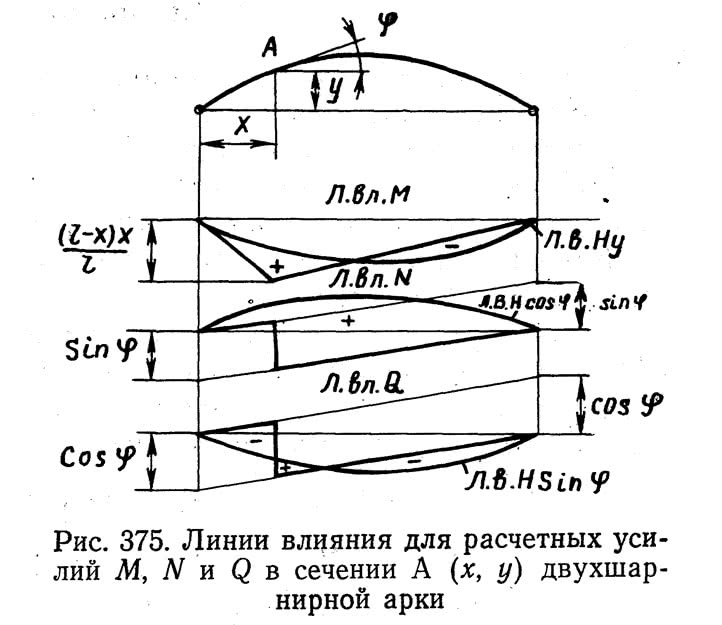
На рис. 375 показаны линии влияния для расчетных усилий М, N и Q в сечении х двухшарнирной арки.

При изменении температуры арки на t градусов по сравнению с температурой ее замыкания в арке возникает температурный распор:

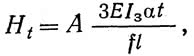
вызывающий в сечении арки с ординатой у изгибающий момент:

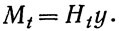
Значение коэффициента линейного расширения а принимают равным 0,000012 (ТУ, п. 132).

I₃ и F₃, необходимые для. построения линий влияния, можно подобрать исходя из приближенного значения усилий в замке арки:

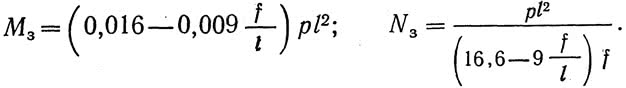
Здесь р — полная (постоянная + временная) нагрузка на 1 пог. м пролета арки.

Линию влияния прогиба арки в четверти пролета в пределах левой полуарки строят на основе равенства:

Здесь ?_? — ордината линии влияния прогиба арки в четверти пролета на расстоянии ? от левой пяты; ?_?⁰ — то же, для основной системы (криволинейной балки); ?_Н — ордината линии влияния распора в том же сечении; ?_H — прогиб основной системы в четверти пролета под действием распора H=1:

Ординаты линии влияния прогибов основной системы в четверти пролета определяются по формулам:

2. Бесшарнирные арки

Бесшарнирная арка трижды статически неопределима. Основную систему образуют обычно по методу сил путем разреза арки в замке на две симметричные части (рис. 376).

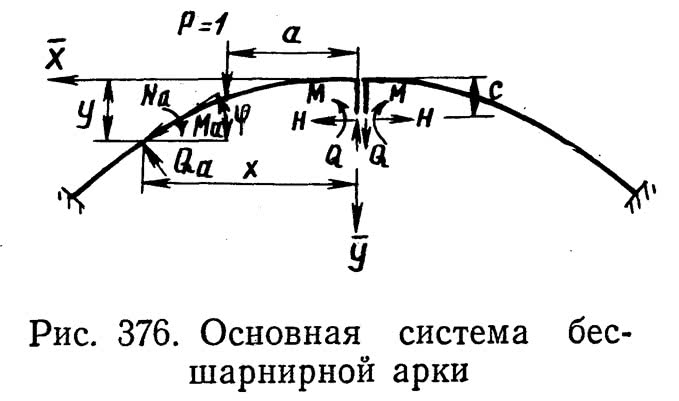
Парные лишние неизвестные Н, М и Q, заменяющие нарушенные разрезкой связи, приложены для исключения побочных перемещений в упругом центре, связанном с торцами полуарок у разреза абсолютно жесткими консолями.

Расчетные усилия в любом сечении арки: момент М_а, продольная сила N_a и поперечная сила Q_a могут быть выражены через соответствующие усилия в том же сечении основной системы (консольной полуарки) М₀, N₀ и Q₀ и лишние неизвестные H, М и Q равенствами:

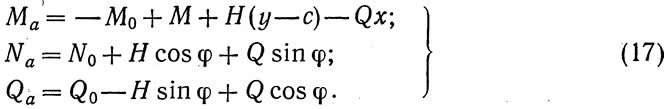
Интегрируя выражения для перемещений, получаем формулы для определения ординат линий влияния для лишних неизвестных для арок пологостью f/l>1/5:

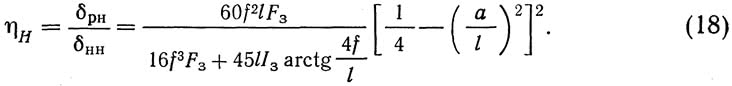
Для арок пологостью f/l2?=1. Тогда формула (18) примет более простой вид:

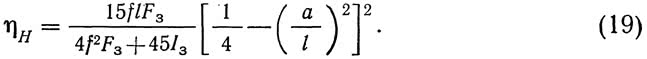
Ординаты линий влияния для момента М и перерезывающей силы вычисляют по формулам:

Усилия M₀, N₀ и Q₀ в сечении х основной системы, загружаемой грузом Р=1 на расстоянии а от начала координат, при положении груза на той же полуарке, где находится сечение х, равны при а х М₀ = х — а, N₀ = sin ?, Q₀ = cos ? при а > х, а также при перемещении груза Р=1 по смежной полуарке М₀ = N₀ = Q₀ = 0. Расстояние упругого центра от начала координат e = 1/3 f.

Температурный распор может быть определен по формулам:

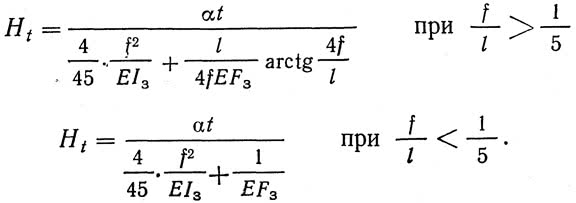
Усилия, вызванные температурными деформациями в сечении арки, будут при этом равны:

Линия влияния для прогиба арки в четверти пролета строится на основе следующих равенств.

Для левого полупролета, предполагая, что сечение х = l/4 находится в этом полупролете,

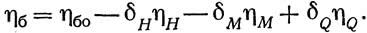
Здесь ?_бо — ордината линии влияния прогиба основной системы; ?_H, ?_M и ?_Q — прогибы арки в четверти пролета при действии единичных усилий в направлении соответствующих лишних неизвестных; ?_H, ?_M и ?_Q — ординаты линии влияния лишних неизвестных H, М и Q, взятые на том же расстоянии а от начала координат (замка арки), на котором находится вычисляемая ордината ?_б.

При перемещении груза по правой полуарке:

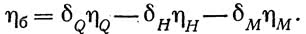
Ординаты линии влияния ?_бо вычисляются по формулам:

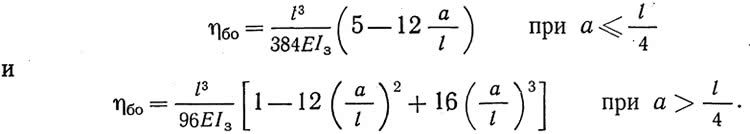
Прогибы ?_H, ?_M и ?_Q определяются по формулам:

3. Гибкая арка с жесткой затяжкой

Для гибкой арки с жесткой затяжкой основную систему удобнее образовать, разрезая не затяжку, а арку (рис. 377).

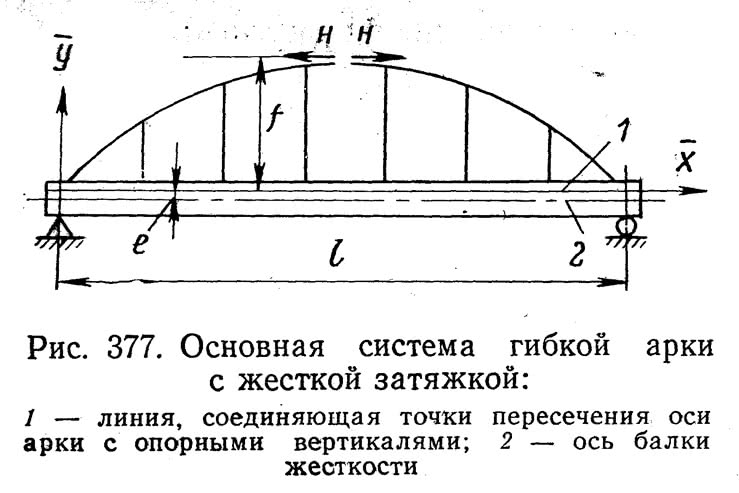
Распор арки приложен вдоль координатной оси х, смещенной относительно нейтральной оси жесткой затяжки кверху на величину е для выравнивания расчетных значений положительных и отрицательных моментов в затяжке.

Уравнение линии влияния распора определится выражением:

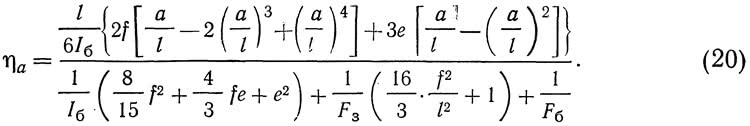
Здесь F_б и I_б — момент инерции и площадь сечения затяжки (балки жесткости), постоянные по длине пролета; F_з — площадь замкового сечения арки.

Усилия в элементах системы определятся по следующим формулам.

Усилие в n-ом стержне арки:

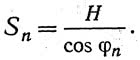
Моменты в балке жесткости (относительно центра тяжести сечения) —

а) в опорном сечении М_оп = —Не;

б) в сечении х

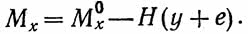
Поперечная сила в сечении х

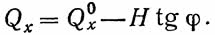
M_x⁰ и Q_x⁰ — момент и поперечная сила в сечении х балки основной системы.

Арка с затяжкой является системой внешне статически определимой, и одинаковое изменение температуры арки и затяжки не вызовет возникновения температурных напряжений. Последние возможны в случаях, когда арка нагревается быстрее или медленнее, чем затяжка, вследствие различных условий обдувания воздухом и защищенности от солнечной радиации. Температурные напряжения этого рода практически не поддаются расчету вследствие сложности и неопределенности температурного поля конструкции.

Линия влияния для прогиба в четверти пролета балки жесткости строится с использованием формул (13), (15) и (16), причем ?_а принимают по формуле (20), а ?_н по формуле:

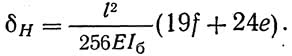
Значение величин I_б, F_б и F_a для подстановки в формулы (20) и (21) можно подобрать по ориентировочным величинам усилий в балке жесткости:

при загружении временной нагрузкой к полупролета:

где q — постоянная погонная нагрузка в балке жесткости и в замковом сечении арки; при загружении полной нагрузкой всего пролета в арке:

Примечания

1. Прокофьев И. П. Теория сооружений, ч. II. М., Трансжелдориздат, 1947.